In this article, we do three things: explain how Notional, TermMax, and Pendle create fixed rates, break down the core mechanics, and compare the design trade-offs side by side.

If you already know the core concepts behind Notional, TermMax, and Pendle, you can jump straight to the comparison table.

Introduction

Variable-rate lending dominates DeFi. Compound, Aave, and dozens of forks let users deposit assets, earn yield, and borrow against collateral with rates that adjust block by block based on pool utilization. This design maximizes capital efficiency: every deposited dollar can be borrowed, and interest rates equilibrate supply and demand automatically. Borrowers pay what the market will bear; lenders accept whatever rate the pool currently offers.

The cost of this efficiency is uncertainty. A borrower who takes a loan at 4% APR today may face 12% next week if utilization spikes. A lender earning 6% can watch returns collapse to 0.5% when borrowing demand evaporates. For users who want to plan cash flows, variable rates introduce unacceptable risk. Traditional finance solved this problem centuries ago with fixed-rate instruments: bonds, term loans, and interest-rate swaps that lock a rate until a known maturity date. DeFi can benefit from the same capability.

The challenge is implementation. Variable-rate pools achieve continuous liquidity and automatic price discovery by pooling all capital into a single shared reserve with dynamic pricing. Fixed-rate systems must somehow preserve liquidity and price discovery while honoring term commitments that cannot be repriced mid-flight.

Notional Finance, TermMax, and Pendle have shipped production implementations, each choosing a fundamentally different architecture. Notional combines an AMM-style liquidity pool for zero-coupon bonds (fCash) with a variable-rate fallback layer (Prime Cash). TermMax uses a peer-to-peer order-matching system where lenders and borrowers negotiate fixed terms on a curve, with each position isolated and collateralized. Pendle splits yield-bearing assets into principal and yield tokens (PT and YT), then trades them on a specialized time-decaying AMM that implicitly encodes fixed rates through PT discounting.

This article walks through the core mechanisms of Notional, TermMax, and Pendle, then compares them across different axes. The goal is not to declare a winner but to make the design choices explicit and show where they create risk or opportunity. Design choices shape liquidity depth, slippage under stress, and capital efficiency.

---

Notional Finance: Core Principles

Notional’s approach to fixed rates rests on a simple insight: if you can trade zero-coupon bonds on-chain, you can extract fixed rates from their discount to par. The protocol implements this through fCash, an accounting unit representing a promise to deliver (positive fCash) or receive (negative fCash) a specific amount of asset at a known maturity date. A user holding +100 fDAI maturing in six months will receive 100 DAI at maturity. A user with -100 fDAI owes 100 DAI at that date. The fixed rate emerges from the price at which fCash trades today relative to its par value at maturity.

To enable trading, Notional runs AMM-style liquidity pools that hold fCash and Prime Cash (a variable-rate money market token). Lenders swap Prime Cash for fCash, paying a discounted price that encodes the fixed yield. Borrowers post collateral and borrow fixed by taking on negative fCash and trading it into the pool, receiving Prime Cash they can withdraw. The pool acts as a continuous market maker, quoting rates based on supply and demand. When lenders dominate, fCash prices rise (rates fall). When borrowers dominate, fCash prices fall (rates rise). The curve adjusts dynamically as trades flow through, similar to Aave but modified to account for time decay as maturity approaches.

Liquidity comes from nToken holders, who deposit assets to mint nTokens representing claims on a portfolio of fCash positions across multiple maturities (typically 3-month, 6-month, 1-year, and 2-year terms) and Prime Cash. The nToken contract automatically mints balanced pairs of positive and negative fCash, deposits the positive fCash into liquidity pools, and retains the negative fCash on its balance sheet. This design means nToken holders are structurally short fixed-rate exposure: they supply the fCash that lenders buy and hold, offsetting debts that settle at maturity. If lending demand outstrips borrowing, nToken holders absorb the imbalance by taking on more debt. The protocol may compensate them with trading fees and NOTE token emissions.

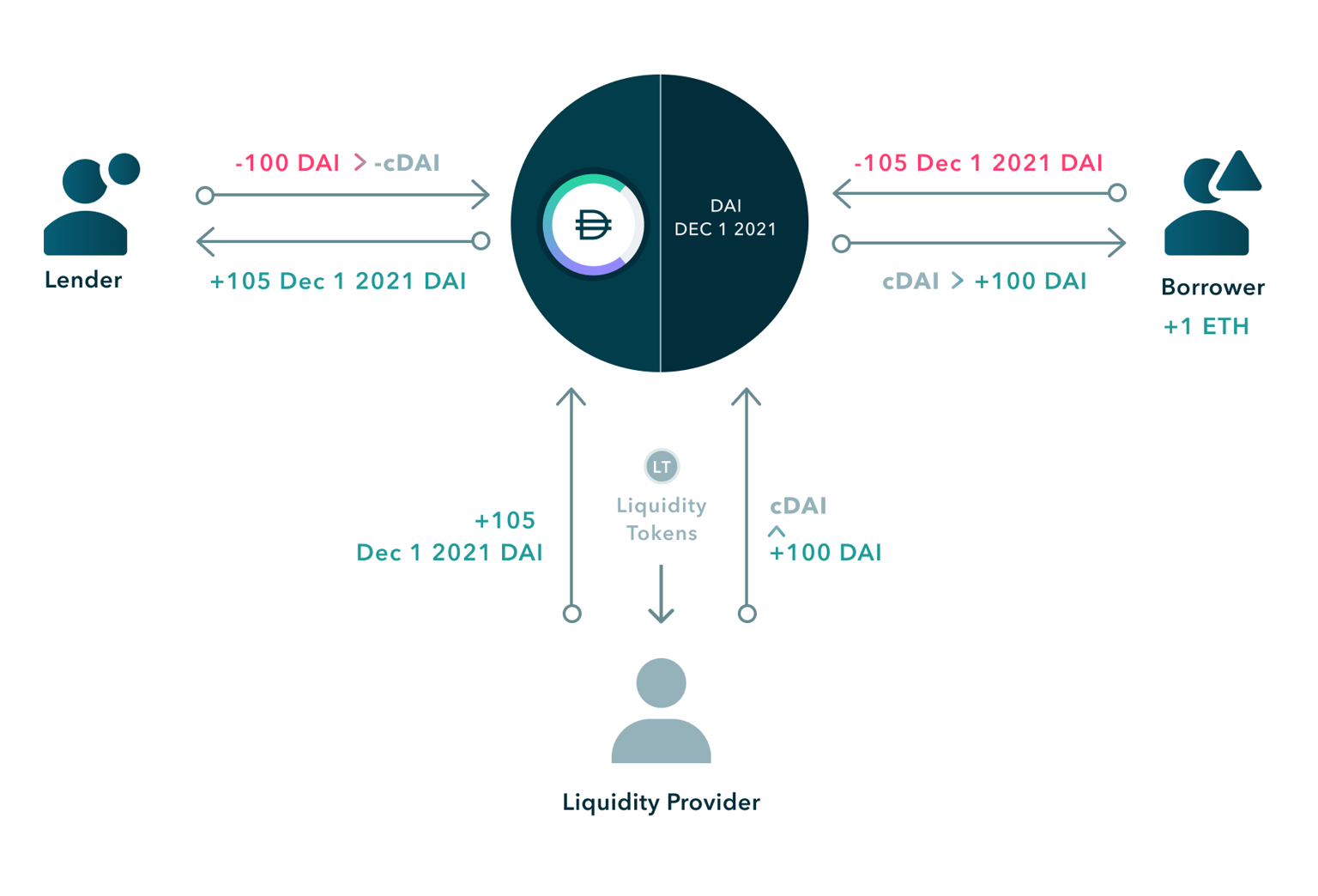
The two-layer structure (Prime Cash as the variable-rate base layer and fCash markets layered on top) creates flexibility. Users who want fixed rates interact with fCash pools. Users who want variable rates use Prime Cash directly. Idle Prime Cash reserves are deployed to external protocols (E.g. Compound, Aave) to earn yield, boosting capital efficiency. At maturity, fCash settles into Prime Cash at the settlement rate, and from that point forward the resulting Prime Cash balance accrues variable rates. Users can hold Prime Cash, withdraw it, or manually trade into a new fCash maturity.

---

TermMax: Core Principles

TermMax takes a maker-taker approach: lenders and borrowers post orders specifying the rates they are willing to accept, and takers execute against chosen orders. FT is fungible within a market and redemption/physical delivery is pro-rata across the market’s pooled collateral, so risk is isolated at the market level. This avoids protocol-wide bad debt but still requires active market makers to provide continuous order flow.

The core mechanism splits each base asset unit into two tokens: a Fixed Token (FT) representing the principal claim, and an Exchange Token (XT) representing the residual or floating component. At any time before maturity, 1 asset unit can be minted into 1 FT + 1 XT, and conversely, 1 FT + 1 XT can be burned back to 1 asset unit. This enforces a pricing identity: P(FT) + P(XT) ≈ 1 in base asset terms. FT trades at a discount before maturity and redeems 1:1 at maturity, so buying FT locks a fixed return. The discount encodes the fixed rate.

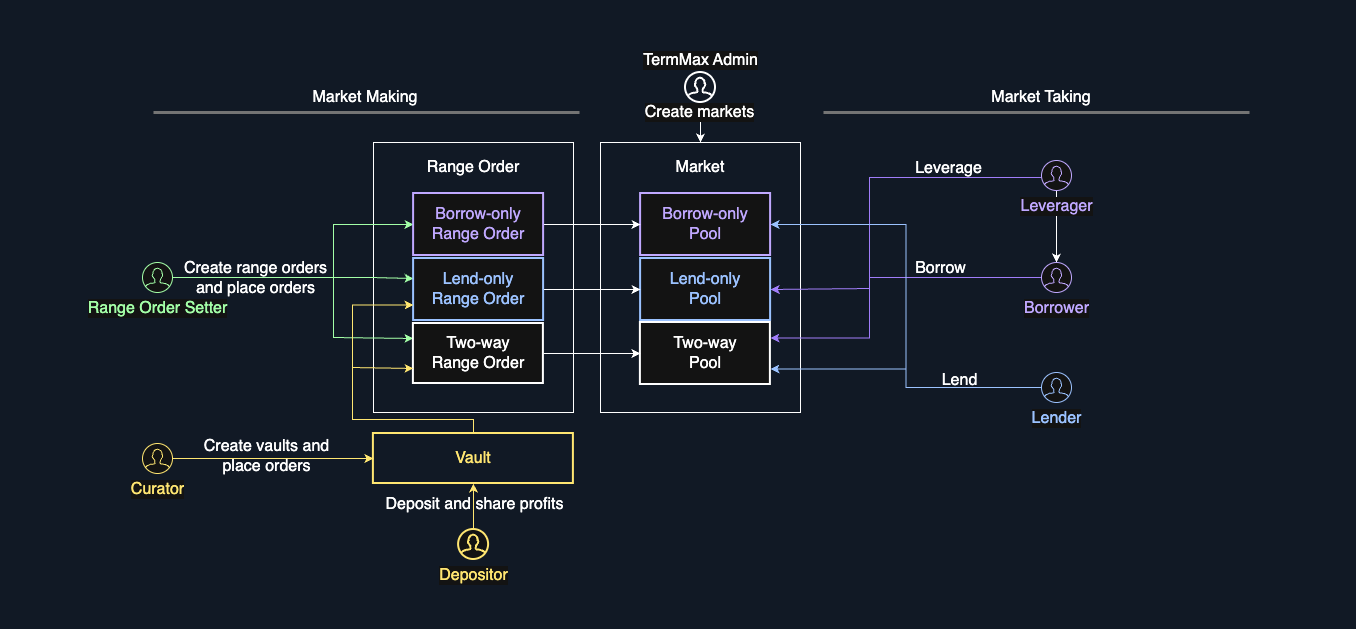
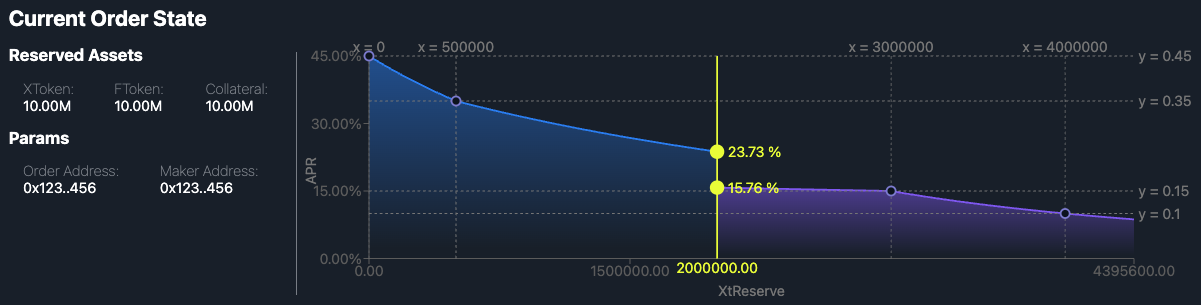
Lenders create range orders by posting piecewise curve cuts and locking capital. Each segment defines virtual reserves, so APR varies continuously with utilization inside the segment. Borrowers post similar curves for borrowing, locking collateral into a Gearing Token (GT), an NFT tracking the collateral balance, debt owed, and maturity. Market takers pass an explicit list of maker orders and execute against them. A borrower taking 3,000 USDC from a lending order locks the rate at the point on that curve corresponding to 3,000 USDC of utilization. The trade is atomic: the lender’s order inventory decreases, the borrower receives funds, and a GT position is opened with the debt denominated in FT terms.

Makers can express sophisticated views through multi-kink curves, adjusting rates based on how much of their capital is utilized. Takers specify slippage bounds (min/max acceptable rate), and if no order can fill within those bounds, the transaction reverts. This is binary execution (fill or fail) rather than the continuous price impact of an AMM.

---

Pendle: Core Principles

Pendle’s design starts from a different question: instead of creating new fixed-rate instruments, what if you decompose existing yield-bearing assets into tradable principal and yield components? While Notional and TermMax originally operate on non-yield-bearing assets (USDC, DAI, ETH) and construct fixed-rate markets from scratch, Pendle works natively with yield-bearing tokens that already generate returns, separating the principal from the yield stream. The protocol wraps yield-bearing tokens (like Aave’s aUSDC or Lido’s stETH) into a Standardized Yield (SY) token, then splits each SY unit into a Principal Token (PT) and a Yield Token (YT). PT is a claim on the principal, redeemable 1:1 at maturity for the accounting asset. YT is a claim on all future yield the underlying generates until maturity. By trading these components separately, users can lock fixed returns (by buying PT at a discount) or speculate on floating yield (by trading YT).

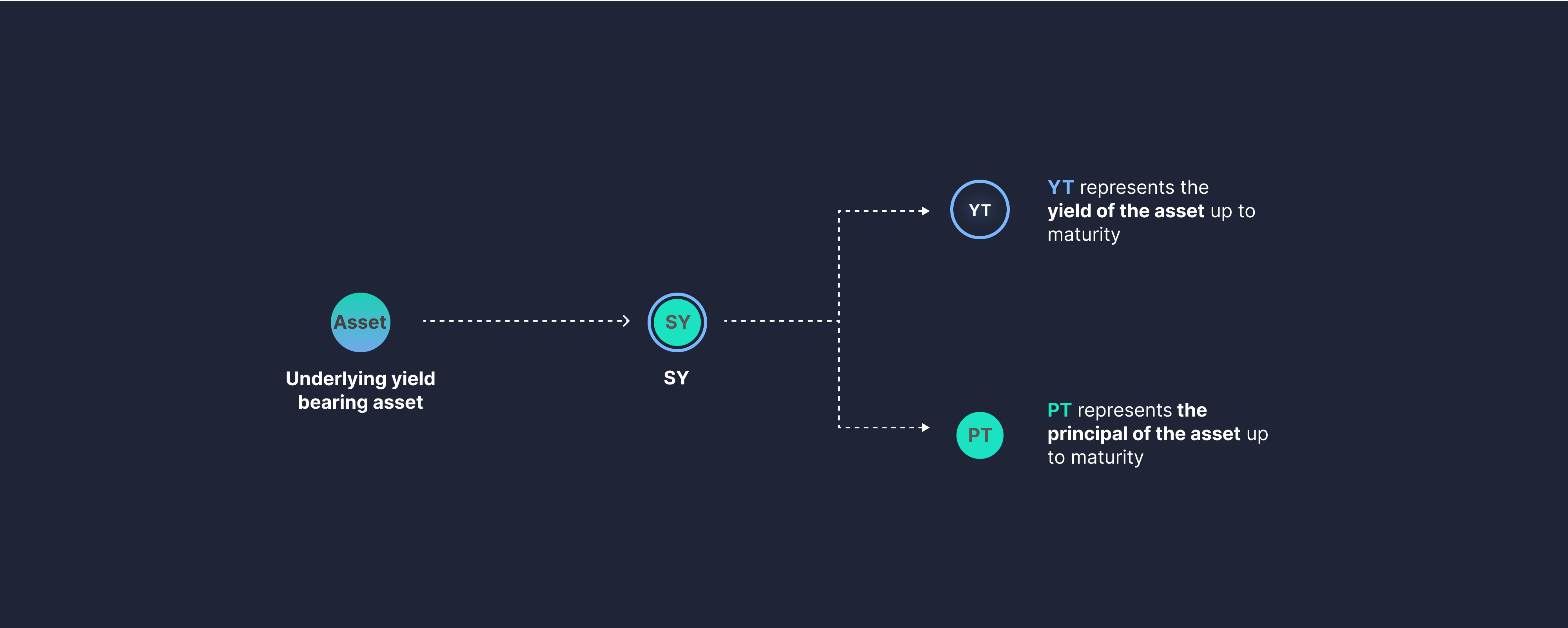
The pricing mechanism relies on a time-decaying AMM that holds PT and SY (not PT and YT directly). The AMM enforces that PT price accretes toward par as maturity approaches, and the discount at any given time encodes the implied fixed rate.

YT trading is more complex because the AMM does not hold YT directly. To buy YT, the router mints PT+YT from the user’s SY, swaps the PT leg into the AMM for additional SY, mints more PT+YT, and balances the flow to deliver net YT. This multi-step process introduces additional price impact and fee layers compared to a direct PT trade, but it allows YT to exist as a liquid instrument without requiring a separate YT/SY pool. YT holders continuously accrue yield from the underlying protocol through an index-based tracking system, and they can sell YT back into the market at any time to exit their floating-rate exposure.

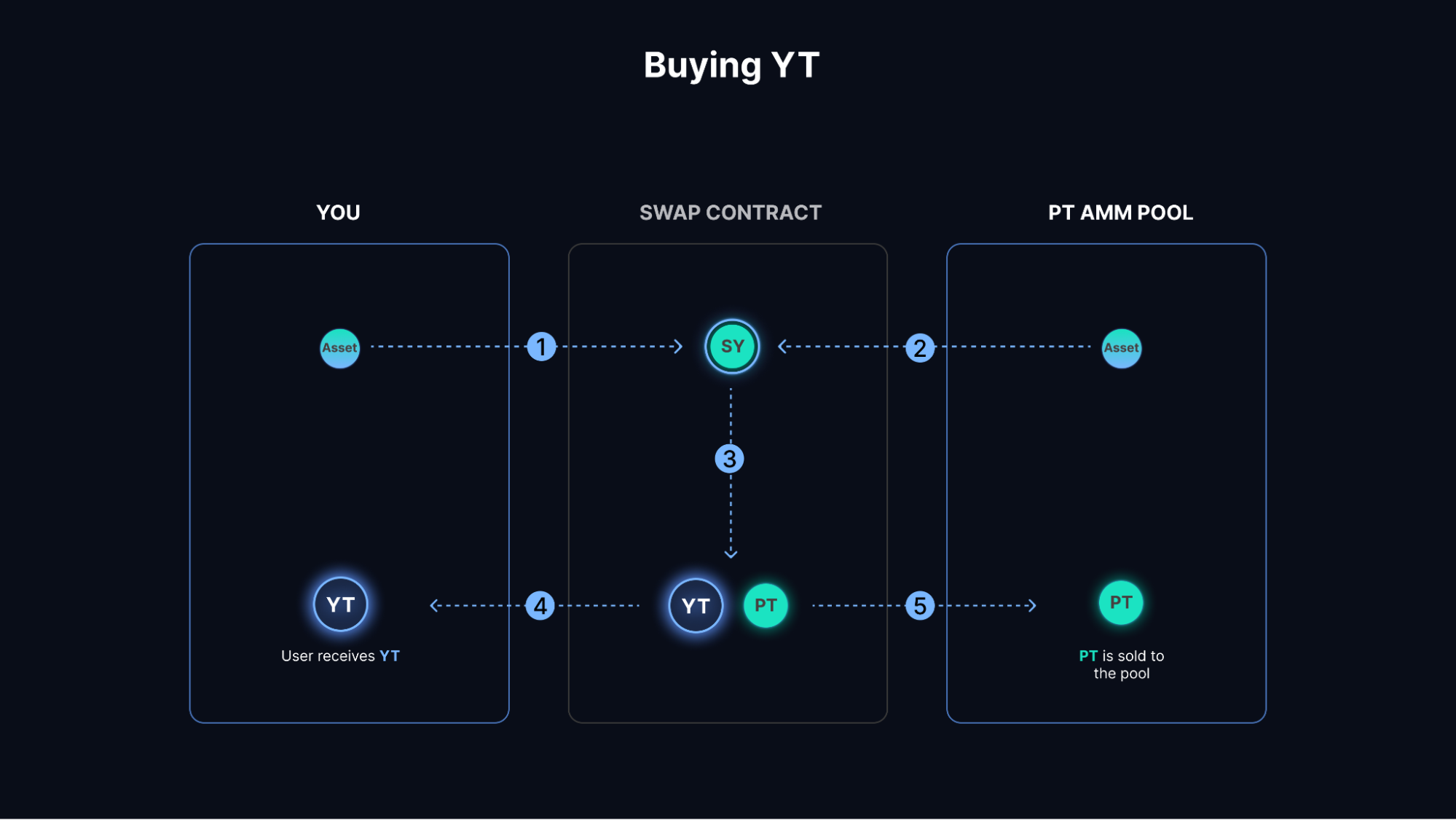
Liquidity provision in Pendle involves depositing PT and SY into the pool (not PT and YT). LPs receive tokens representing claims on both reserves plus accrued fees. They earn from three sources: PT’s natural accretion toward par, the underlying yield generated by SY in the pool (e.g., staking rewards from stETH), and swap fees charged on trades. LPs face basis risk if implied rates shift significantly, but PT and SY are highly correlated and converge at maturity, which can reduce divergence risk relative to unrelated assets. The code limits pool imbalance to 96% of reserves to prevent destabilization.

Pendle’s design prioritizes composability and capital efficiency. PT and YT are standard ERC20 tokens that can be integrated into other DeFi protocols as collateral, yield sources, or trading instruments. The protocol has shipped PT oracles to support safe collateral usage downstream. The hybrid AMM plus optional limit-order system allows sophisticated market makers to post signed orders at specific implied rates, improving execution for large trades without locking capital into the pool. Cross-chain deployments (Ethereum, Arbitrum, and other L2s) rely on LayerZero messaging to broadcast governance results, introducing a dependency on that infrastructure’s liveness.

---

With the core mechanisms established, we can now compare how each protocol handles the same operational challenges.

---

Comparison

Fixed-Rate Calculation

Fixed rates across these three protocols emerge through fundamentally different mechanisms, each with distinct implications for how liquidity providers participate and how rates respond to market conditions.

Notional

Notional calculates fixed rates through a piecewise linear interest rate curve that determines the interest rate based on market utilization. Utilization is defined as $p=\frac{\text{total fCash}\pm \text{fCash to account}}{\text{total fCash}+\text{total cash}}p\; =\; \backslash frac\{\backslash text\{total\; fCash\}\; \backslash pm\; \backslash text\{fCash\; to\; account\}\}\{\backslash text\{total\; fCash\}\; +\; \backslash text\{total\; cash\}\}$ (InterestRateCurve.sol#L239-L251).

The interest rate curve uses a three-segment piecewise linear function with two kink points (InterestRateCurve.sol#L267-L288):

where $k_1,k_{2}k\_1,\; k\_2$ are kink utilization points, $r_1,r_{2}r\_1,\; r\_2$ are kink rates, and $r_{max}r\_\{max\}$ is the maximum rate. This design is similar to Compound/Aave's interest rate models.

The interest rate $rr$ relates to the exchange rate via $\text{exchangeRate}=e^{rt}\backslash text\{exchangeRate\}\; =\; e^\{rt\}$, where $tt$ is time to maturity (InterestRateCurve.sol#L516-L529). This exchange rate determines how much Prime Cash is needed to purchase a given amount of fCash.

TermMax

TermMax calculates fixed rates through individual order curves where each order operates as a constant-product AMM with piecewise segments (kinks). Makers (lenders/borrowers) configure curves by specifying segments, each defined by three parameters: xtReserve (boundary position where the segment starts), liqSquare (L², the liquidity parameter), and offset (β, a virtual reserve offset).

The protocol calculates virtual reserves as

$$\text{vXtReserve}=\text{xtReserve}+\beta \text{andvFtReserve}=L^2\mathrm{/}\text{vXtReserve}\backslash text\{vXtReserve\}\; =\; \backslash text\{xtReserve\}\; +\; \backslash beta\; \backslash text\{and\}\; \backslash text\{vFtReserve\}\; =\; L^2\; /\; \backslash text\{vXtReserve\}$$

(TermMaxCurve.sol#L38-L49). The instantaneous APR at any point is

$$\text{APR}=(\text{vFtReserve}\mathrm{/}\text{vXtReserve})\times (365\mathrm{/}\text{daysToMaturity})\backslash text\{APR\}\; =\; (\backslash text\{vFtReserve\}\; /\; \backslash text\{vXtReserve\})\; \backslash times\; (365\; /\; \backslash text\{daysToMaturity\})$$

(TermMaxOrderV1Plus.sol#L197-L199, #L208-L210), representing the annualized rate at current reserves.

All trades within a segment follow constant-product AMM mechanics:

$$\text{vXtReserve}\times \text{vFtReserve}=L^2\backslash text\{vXtReserve\}\; \backslash times\; \backslash text\{vFtReserve\}\; =\; L^2$$

Buying tokens uses the direct formula

$$\mathrm{\Delta }\text{out}=\text{vReserveout}-L^2\mathrm{/}(\text{vReservein}+\text{input})\backslash Delta\backslash text\{out\}\; =\; \backslash text\{vReserve\}\{\backslash text\{out\}\}\; -\; L^2\; /\; (\backslash text\{vReserve\}\{\backslash text\{in\}\}\; +\; \backslash text\{input\})$$

(TermMaxCurve.sol#L294), while selling tokens solves the quadratic derived from the same invariant (TermMaxCurve.sol#L275-L281). Larger trades cause greater slippage as reserves shift along the curve.

When a trade exhausts the current segment, execution moves to the next kink. The protocol enforces continuity between segments using

$$L^{\mathrm{\prime }2}=L^2\times [(x^{\mathrm{\prime }}+{\beta }^{\mathrm{\prime }}{)}^2\mathrm{/}(x^{\mathrm{\prime }}+\beta {)}^2]L\text{'}^2\; =\; L^2\; \backslash times\; [(x\text{'}\; +\; \backslash beta\text{'})^2\; /\; (x\text{'}\; +\; \backslash beta)^2]$$

(TermMaxOrderV1Plus.sol#L268-L286), where x' is the boundary position (xtReserve at the kink), β and β' are the old and new offsets, and L² and L'² are the old and new liquidity parameters. This ensures the rate remains continuous at boundaries with no jumps between segments. The iteration through segments is handled by forward and reverse traversal functions (TermMaxCurve.sol#L59-L99, #L109-L146).

The effective rate a user receives depends on starting reserves (which determine the initial APR), trade size (which determines slippage along the curve), and how many kinks the trade crosses. Unlike a simple "4% flat for 5,000 USDC" model, the actual rate follows AMM mechanics: it starts around 4% and degrades continuously as reserves shift within each segment.

Pendle

Pendle extracts fixed rates from PT discounts in a time-decaying AMM. The pool holds PT and SY, not PT and YT. The AMM calculates the exchange rate using a logit-based curve:

$$\text{exchangeRate}=\frac{\ln (p\mathrm{/}(1-p))}{s}+a,\text{where }p=\frac{\text{PT}}{\text{PT}+\text{totalAsset}}\backslash text\{exchangeRate\}\; =\; \backslash frac\{\backslash ln(p/(1-p))\}\{s\}\; +\; a,\; \backslash text\{where\; \}\; p\; =\; \backslash frac\{\backslash text\{PT\}\}\{\backslash text\{PT\}\; +\; \backslash text\{totalAsset\}\}$$

is the pool proportion (MarketMathCore.sol#L354-L373). The rate scalar $s=\frac{s_{\text{root}}\times 365}{\text{timeToExpiry}}s\; =\; \backslash frac\{s\_\{\backslash text\{root\}\}\; \backslash times\; 365\}\{\backslash text\{timeToExpiry\}\}$ increases as maturity approaches (MarketMathCore.sol#L383-L386), making the curve steeper and amplifying price impact near expiry.

The rate anchor $aa$ is dynamically computed to ensure the curve passes through the last traded implied rate. It is recalculated after each trade as:

$$a=E_{\text{last}}-\frac{\ln \left(\frac{p_{\text{current}}}{1-p_{\text{current}}}\right)}{s},\text{where }{E}_{\text{last}}=e^{r_{\text{last}}\times t\mathrm{/}365}a\; =\; E\_\{\backslash text\{last\}\}\; -\; \backslash frac\{\backslash ln\backslash left(\backslash frac\{p\_\{\backslash text\{current\}\}\}\{1-p\_\{\backslash text\{current\}\}\}\backslash right)\}\{s\},\; \backslash text\{where\; \}\; E\_\{\backslash text\{last\}\}\; =\; e^\{r\_\{\backslash text\{last\}\}\; \backslash times\; t\; /\; 365\}$$

and $r_{\text{last}}r\_\{\backslash text\{last\}\}$ is the last implied rate (MarketMathCore.sol#L305-L323).

The implied rate is then extracted

$$\text{lnImpliedRate}=\frac{\ln (\text{exchangeRate})\times 365\text{ days}}{\text{timeToExpiry}}\backslash text\{lnImpliedRate\}\; =\; \backslash frac\{\backslash ln(\backslash text\{exchangeRate\})\; \backslash times\; 365\; \backslash text\{\; days\}\}\{\backslash text\{timeToExpiry\}\}$$

(MarketMathCore.sol#L327-L341).

Note: AMM-based models (Notional, Pendle) guarantee execution at a price determined by pool state, but large trades incur slippage that can make effective rates worse than advertised. Order-book models (TermMax) offer tighter spreads when liquidity is deep, but execution can fail if no maker is willing to fill at acceptable rates. Near maturity, Pendle’s amplified price impact and Notional’s utilization-based adjustments can cause rate spikes under stress.

---

---

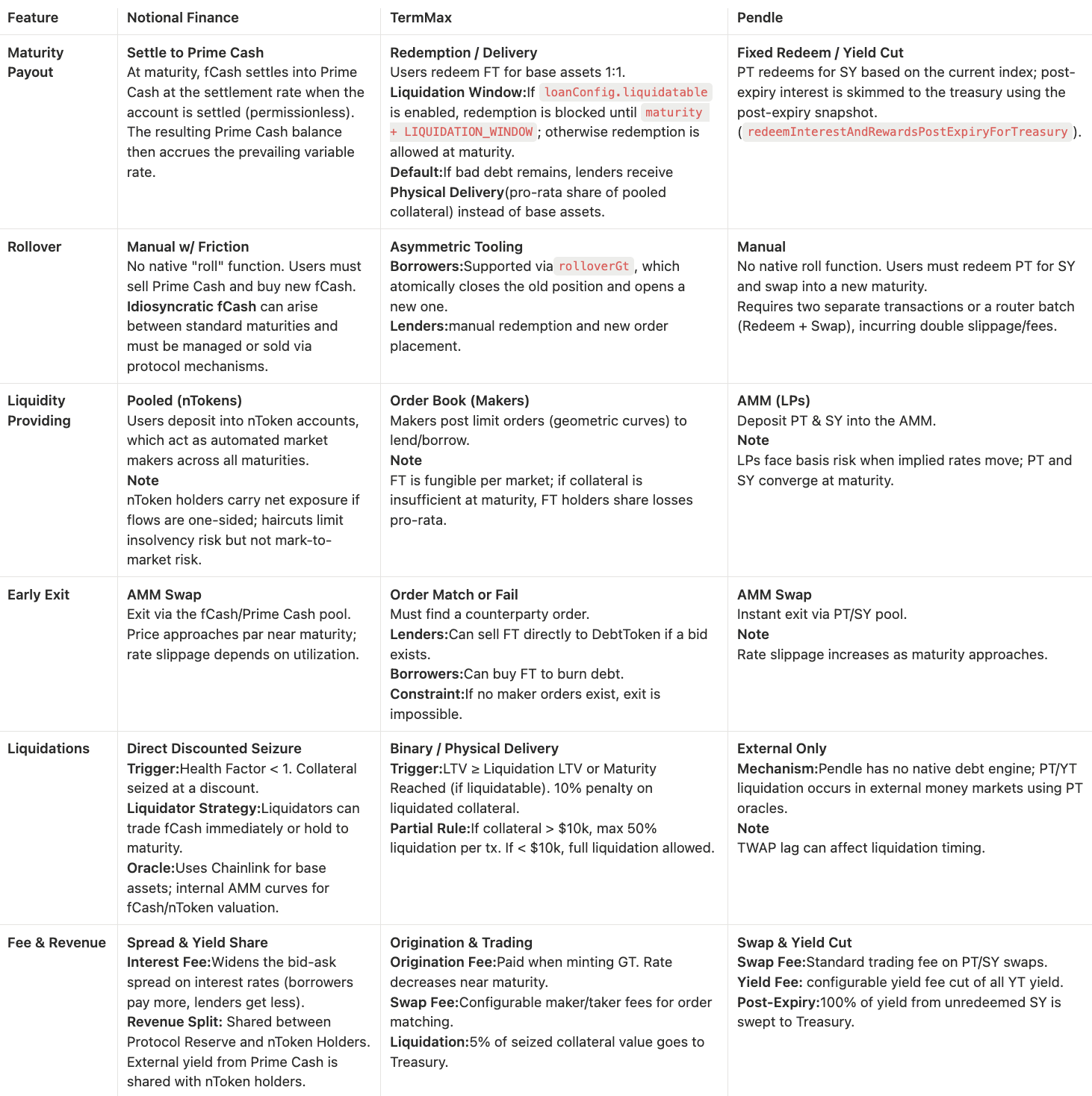
Notable Features

Beyond the core fixed-rate mechanisms, each protocol ships design choices that reveal architectural priorities and create opportunities or constraints for integrators and users.

Notional

Notional’s batch transaction system allows multiple actions (deposits, trades, borrows, collateral adjustments) to execute atomically with netted settlement. The protocol tracks deltas throughout the batch and settles all transfers at the end, reducing gas costs and enabling complex multi-leg strategies in a single transaction. In practice, the batching infrastructure is most valuable for programmatic integrators building multi-leg strategies, since many retail flows are single‑action. However, batching allows implementing interesting features for UI, like the seamless roll between markets. The quarterly market rebalancing mechanism (where expiring fCash markets roll forward and liquidity transfers to new maturities) automates what would otherwise require manual LP migrations. However, it introduces “idiosyncratic fCash” (ifCash) positions that do not fit into active markets and must be valued via oracle, creating a long tail of residual positions that nToken holders must manage or sell at a discount.

TermMax

TermMax’s physical delivery mechanism for defaults is unusual in DeFi. Instead of socializing bad debt across a pool or maintaining an insurance fund, lenders receive collateral tokens proportional to their FT holdings when borrowers fail to repay. This eliminates protocol-level insolvency risk but requires lenders to handle potentially illiquid or volatile collateral assets. A lender who extended USDC expecting to receive USDC back, may instead receive WETH or another collateral token at a loss if the borrower defaulted. This design choice reflects a market-level risk model: participants share default outcomes pro-rata within a market.

TermMax also offers one-click leverage, where users provide collateral and specify a multiplier (e.g., 3x). The protocol takes a flash loan of the debt token, buys more collateral on a DEX, locks it all into a GT, and mints FT only as a leverage fee to the treasurer. Passive LPs can deposit into ERC4626 vaults managed by curators who allocate capital across orders, rebalance as markets shift, and charge performance fees. Vault depositors rely on curator skill and share any losses from defaults via physical delivery.

Pendle

Pendle’s PT oracle system exposes TWAP feeds that allow downstream protocols to use PT as collateral safely. This composability is critical for PT adoption beyond Pendle’s own markets: if other lending protocols can price PT accurately, it becomes a productive asset that can collateralize further borrowing. The oracle design must balance manipulation resistance (TWAP smoothing over a window) with responsiveness (catching sharp rate moves before liquidations are needed). The limit-order system coexisting with the AMM provides an escape valve for large trades: sophisticated makers can quote tighter spreads than the AMM without locking capital into the pool, improving capital efficiency for participants willing to manage off-chain order refreshing.

---

Conclusion

Protocol choice depends on the use case and risk appetite. Notional suits users who value continuous liquidity and are comfortable with AMM slippage. The two-layer Prime Cash design provides flexibility, and the automatic conversion of fCash to variable-rate exposure at maturity simplifies accounting for users who do not want to actively manage rollover. Integrators building on Notional benefit from batch transactions and composability with external yield sources.

TermMax suits lenders and borrowers who prefer isolated risk and are willing to accept liquidity uncertainty in exchange for competitive maker-driven rates. The peer-to-peer model avoids pooled LP risk but requires active market makers to maintain order flow. Physical delivery eliminates protocol insolvency but pushes collateral risk onto lenders, who must be prepared to receive and manage non-stable assets. Integrators should evaluate whether the vault system (curator-managed ERC4626 pools) provides sufficient liquidity for their use case, or if direct order posting is required.

Pendle suits users who want composable yield instruments. The PT/YT split enables sophisticated strategies and integrates cleanly with other DeFi protocols via standard ERC20 interfaces. The time-decaying AMM guarantees liquidity but amplifies slippage near maturity, so users planning large trades or exits should act well before expiry. Integrators using PT as collateral elsewhere must trust Pendle’s oracle implementation and understand that liquidation timing in downstream protocols depends on TWAP lag.

Open questions remain for security reviewers. How do the systems behave when oracle feeds stall during network congestion? Can liquidators execute profitably under gas price spikes, or will positions go underwater before liquidation completes? How do rollover frictions compound when multiple markets mature simultaneously and liquidity concentrates into a narrow time window? Each protocol’s answer to these questions shapes its resilience profile.

Fixed-rate lending in DeFi is not a solved problem. The architectures explored here represent different points on the trade-off curve between liquidity guarantees, rate competitiveness, capital efficiency, and risk isolation. Recognizing trade-offs is the starting point for evaluating whether a fixed-rate system will hold up under stress, and whether its invariants, oracle dependencies, and governance levers create acceptable risk for your use case.

---

Special thanks to the teams at @Pendle_fi, especially RightSide, and @NotionalFinance, especially Jeff Wu, for their time, feedback, and assistance.